
Lagrange Points
When I was in high school physics class learning about gravity, I recall wondering if we could determine the size, or at least the mass, of the universe by calculating how much gravitational pull the planet “feels.” If the planet is tugged more in one direction, could we determine where we are in the universe? If we’re exactly in the center, the yank from the mass of the cosmos would be balanced. If we were on an edge, we might feel the jerk all in one direction. Although the general idea is sound, it’s extraordinarily oversimplified, likely impossible to measure, and misses some key components to gravity.
The main problem with the notion is gravitational force is inversely proportional to the square of the separation distance between the two objects in question. The farther two masses are from each other, the weaker the gravitational pull. Because it’s squared, the force becomes incredibly weak over long distances, rendering my universe-wide gravitational measurements moot. Though I had no idea then, I was, at least, thinking about an interesting line regarding gravity.
Is there a spot where the pull from two massive objects would be in equilibrium? Adding a third body to the mix, could I float someplace in space where the gravity from the sun and the gravity from the Earth would equal each other? As we learned in our previous exploration of the James Webb Space Telescope, the answer is yes!
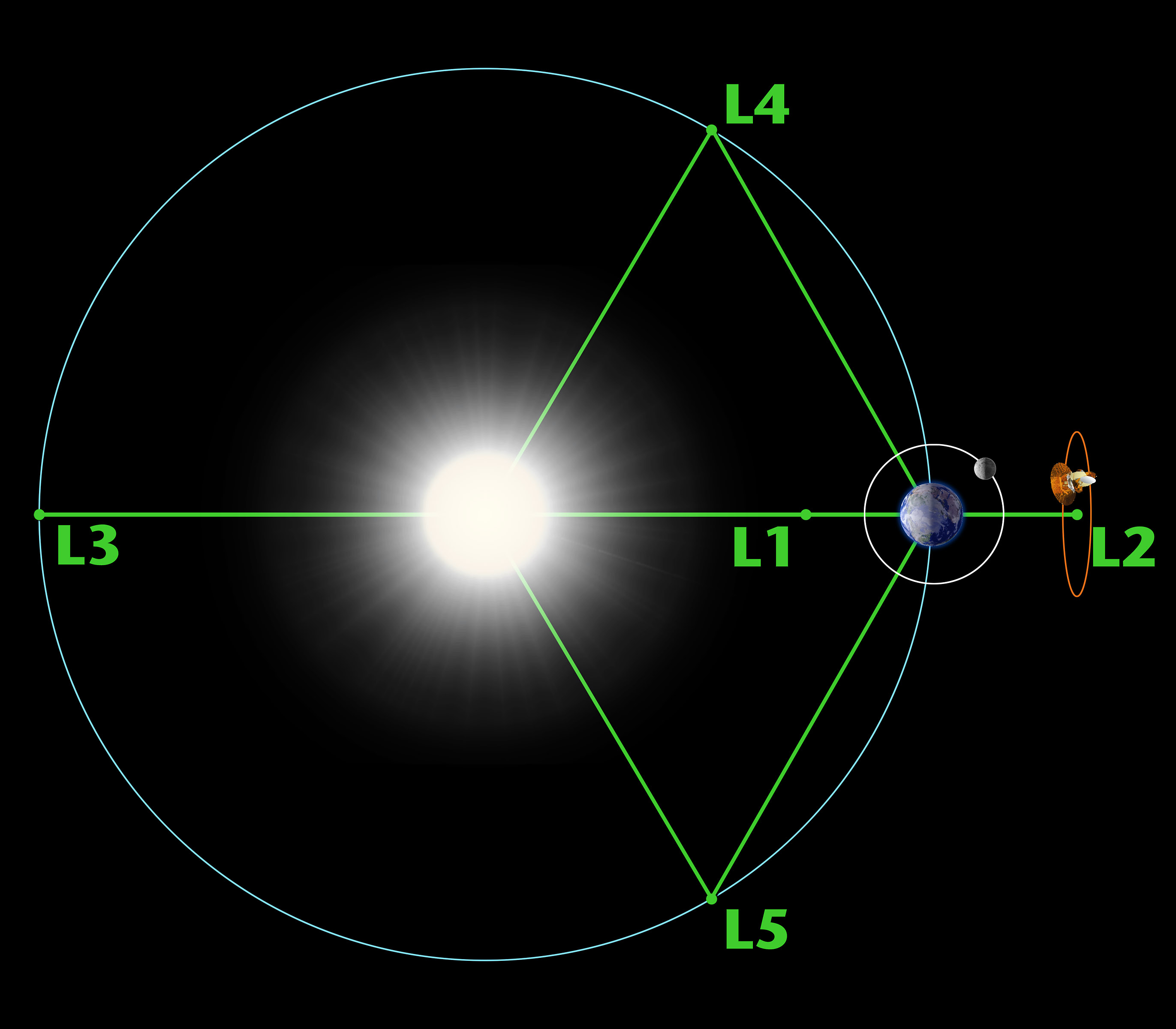
Lagrange points are locations in space where an object of small mass can reach gravitational equilibrium between two larger bodies. As it turns out, two massive entities have five Lagrange points, which astronomers abbreviate as L1 through L5. We’ll skip the mathematics for the sake of brevity, but these points were discovered as exercises in the celebrated three-body problem, which seeks to understand how three objects will react to one another. Famous mathematician Leonhard Euler discovered the first three points of equilibrium. Italian mathematician Joseph-Louis Lagrange worked out the final two points that now share his name. Why did Euler get the short end of the name game? Euler seems to be constantly underrated when it comes to monsters of the maths. Regardless, Lagrange points are what we roll with!
Anything at one of the points labeled in the graphic above will find itself in relative stability. Closer to the Earth than the point and the object will move toward the planet; closer to the sun and the star’s influence will win. Though we highlight the points in the Sun-Earth system, any two large bodies will feature five Lagrange points. Every planet in the solar system has five points related to the sun. Our planet and our moon have five Lagrange points, separate from those we share with the sun.
Points L1, L2, and L3 reside on a line through the center of the two masses. The fourth and fifth points form a nice equilateral triangle with the centers of the two major bodies.

Once humanity acquired the ability to send craft into space, these Lagrange points moved from mathematical curiosities to practical powerhouses. Because of the stability of the points, they are perfect locations for artificial satellites.
You’ll notice in the earlier description, however, that I cited “relative stability” of the points. In fact, the first three points are not completely steady locations for an object. They come close, but something cannot remain in place indefinitely there. Many satellites at these locales come packed with minimal propellant to keep them in range. Further, an object can enter what is known as a halo orbit around the Lagrange point. By circling the point, a satellite can remain in equilibrium.
This maneuver is exactly what the James Webb Space Telescope is on its way to achieving. We sent the craft to L2, where it will embark upon a halo orbit. Watch the following video to visualize Webb’s movement around the sun:
The fourth and fifth Lagrange points, unlike their brethren, are mighty nexuses of stability.
They are so steady that they actually swallow interstellar debris, almost as if they were massive bodies. Any object trapped at L4 or L5 we call trojan asteroids. Jupiter, for example, has more than a million trojan asteroids at its fourth and fifth Lagrange points. In the Sun-Earth system, we have two captured asteroids – 2010 TK7 and 2020 XL5 – and the Earth-Moon system features amalgamations of interplanetary dust, called Kordylewski clouds.
Say that one three times quickly.
As the James Webb Space Telescope zooms to our second Lagrange point, may we all find junctures of equilibrium around which we can orbit!
Further Reading and Exploration
What is a Lagrange Point? – NASA Solar System Exploration
Lagrange Points: Parking Places in Space – Space.com
James Webb Space Telescope – Official website
‘L2’ Will be the James Webb Space Telescope’s Home in Space – NASA














Gravity does not cancel out at any of the Lagrange points. At L2 the central and orbiting body are both pulling the same direction.
Only at L1 do the two bodies pull the opposite direction. However the central body’s pull is stronger at L1. In the case of the sun earth L1, the sun’s pull is 34 times as strong at L1.
It is a 3 man tug of war, the 3rd man being centrifugal force. Many teachers are reluctant to use this term because it’s not really a force but inertia in a rotating frame. But if you happen to be in that frame it sure feels like a force.
You’re completely right. I didn’t do a great job of “explaining like I’m five” on this one. I will rework a few passages. It’s a tough balance to get all the science completely right while using language that works in a frequent newsletter. Thank you for the post!
Pingback: A Big Week for Astrophotography – themountainsarecalling.earth